Álgebra de funciones Álgebra YouTube

Una función algebraica es una función matemática cuyos valores se obtienen mediante operaciones algebraicas (sumas, restas, multiplicaciones, divisiones y potencias) aplicadas a una variable o varias variables. Estas funciones se expresan mediante fórmulas algebraicas que involucran coeficientes y constantes.
FUNCIONES. Algebraicas. Racionales. Características, Dominio YouTube

Función algebraica. En matemáticas, una función algebraica es una función que satisface una ecuación polinómica cuyos elementos son a su vez polinomios o monomios. Por ejemplo, una función algebraica de una variable x es una solución y a la ecuación. , donde los coeficientes a ( x) son funciones polinómicas de x.
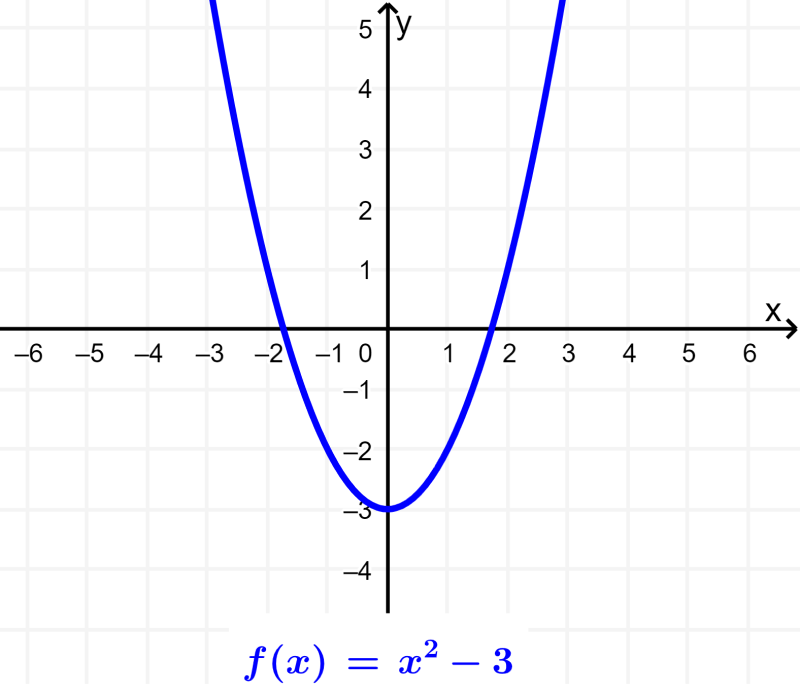
Tipos de Funciones Algebraicas y sus Gráficas Neurochispas
20 unidades · 405 habilidades. Unidad 1 Introducción al álgebra. Unidad 2 Resolución de ecuaciones básicas y desigualdades (una variable, lineal) Unidad 3 Ecuaciones lineales, funciones y gráficas. Unidad 4 Sucesiones. Unidad 5 Sistemas de ecuaciones. Unidad 6 Desigualdades con dos variables. Unidad 7 Funciones.
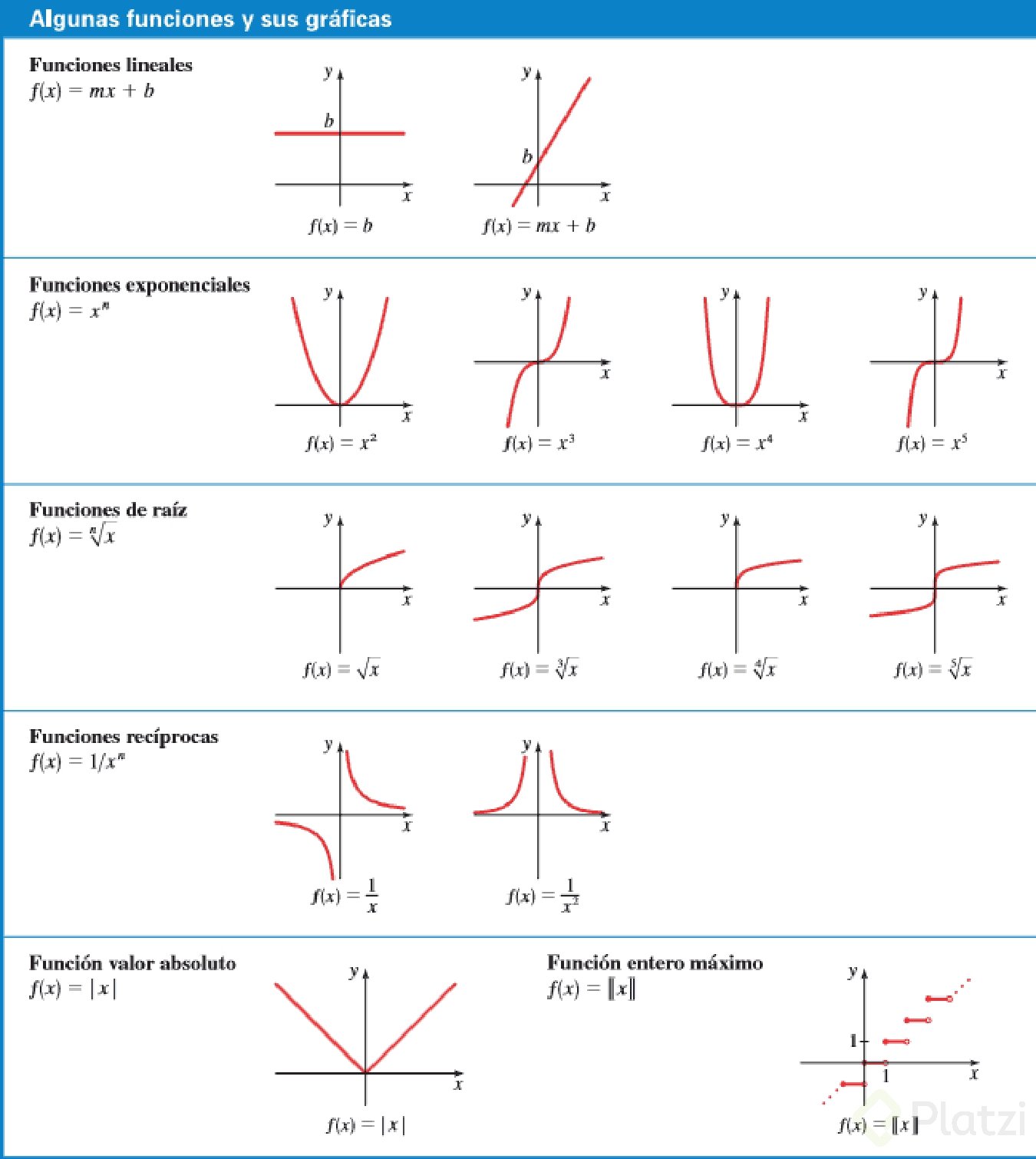
Funciones GráFicas
Definición de Función Algebraica: Una función algebraica es una relación entre dos o más conjuntos de elementos, donde un conjunto se denomina domino, y el otro se denomina codominio.Esta relación se puede expresar como una ecuación o una expresión algebraica. La función algebraica se usa para modelar procesos matemáticos y para representar relaciones entre variables.
Límites de funciones algebráicas Ejemplo 4 YouTube
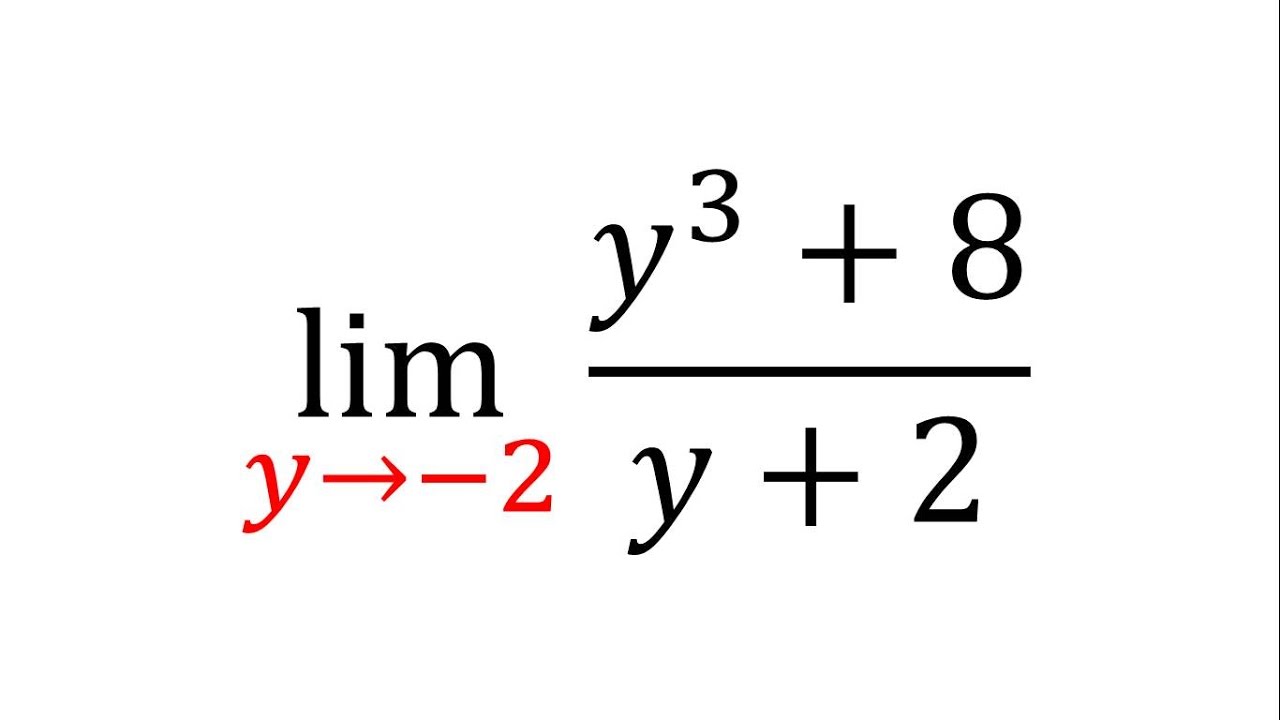
Podríamos decir que una función es una regla que asigna un objeto único en su rango a cada objeto en su dominio. Tomemos por ejemplo, la función que mapea cada número real a su cuadrado. Si nombramos la función f, entonces f mapea 5 a 25, 6 a 36, −7 a 49, y así sucesivamente. En símbolos, escribiríamos.
Límites de funciones algebráicas Ejemplo 2 YouTube
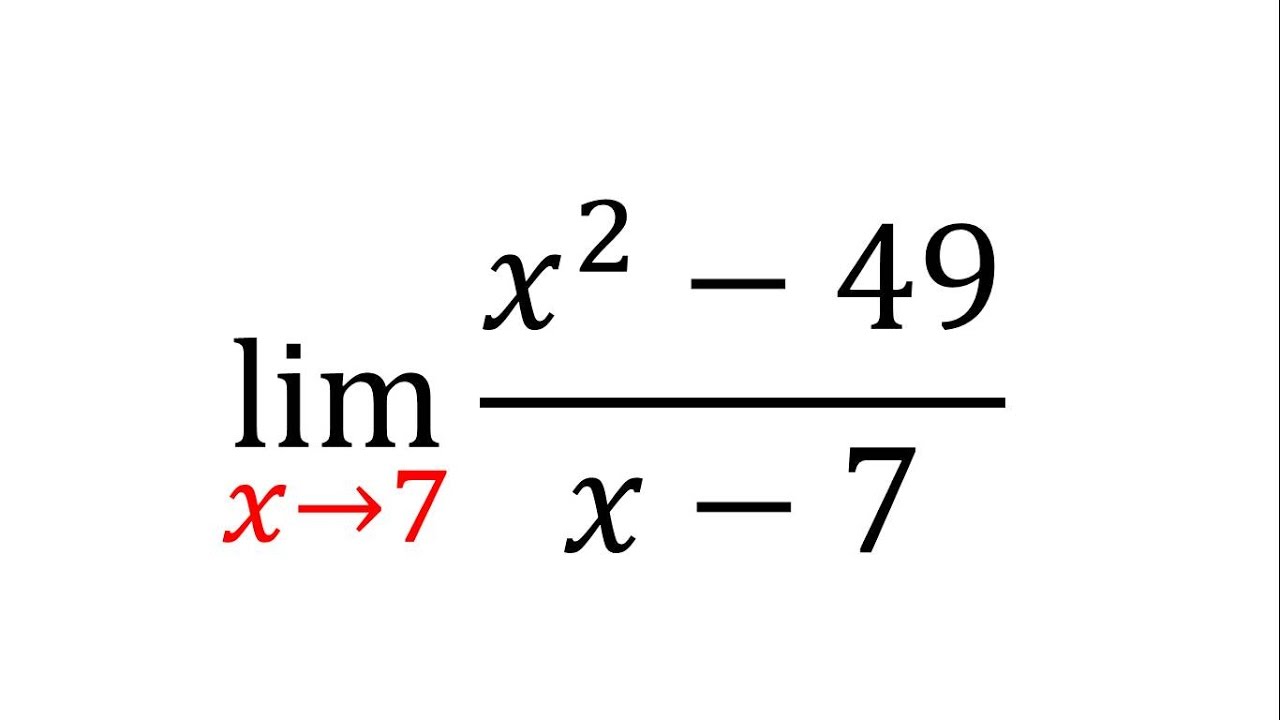
Transcripción del video. una función de la cual hablaré en términos un poco abstractos en esta ocasión es algo una función es algo que va a recibir una entrada entrada va a trabajar con esa entrada la va a manipular y con base en la naturaleza de esta entrada va a generar o va a entregar cierta salida veamos un ejemplo de una función voy.
REPRESENTACIÓN DE FUNCIONES [DIAGRAMA SAGITAL, TABLA, GRÁFICA Y ALGEBRAICA] YouTube

Max Hoyos 14 de agosto de 2020. Las funciones algebraicas es un tipo de regla que relaciona un conjunto de valores (valores independientes, "x") con otro conjunto de valores (valores dependientes, "y") a través de una ecuación algebraica. Es decir, a una ecuación algebraica (y = ax n + bx + c) se van proporcionando valores (x) y.
¿Qué son las funciones y para qué sirven?
Escalar y reflejar funciones de valor absoluto: la gáfica. (Abre un modal) Graficar funciones de valor absoluto. (Abre un modal) Repaso de gráficas de valor absoluto. (Abre un modal) Introducción a funciones definidas por partes. (Abre un modal) Ejemplo resuelto: evaluar funciones definidas por partes.
Funciones algebraicas YouTube

Función lineal. Todas las funciones de la forma f (x)=ax+b f (x) = ax + b, en donde a y b son números reales y a es diferente de cero, son funciones lineales. La gráfica de estas funciones siempre será una línea recta. Esto significa que la función lineal es una función polinómica de primer grado:
Integral de una función algebraica ejercicio 1│Integral algebraica 2 de 8 YouTube

Notación de funciones. La notación y = f(x) define una función llamada f. Esto se lee como " y es una función de" x. La letra x representa el valor de entrada, o variable independiente. La letra y, o f(x), representa el valor de salida, o variable dependiente. Ejemplo 3.2.3: Using Function Notation for Days in a Month.
Función lineaL. Gráfica de una función. Ejercicios. Tabulación. Función algebraica. YouTube

Tenemos la opción de encontrar primero la suma o diferencia en general y luego usar la función resultante para evaluar para la variable dada, o evaluar cada una primero y luego encontrar la suma o diferencia. Ejemplo 4.1.5. Evaluar (f − g)(3) dado f(x) = 5x2 − x + 4 y g(x) = x2 + 2x − 3. Solución.
Como calcular el dominio de funciones algebraicas YouTube

Antes de adentrarnos en la clasificación y la representación gráfica, es importante comprender qué se entiende por funciones algebraicas. En términos sencillos, una función algebraica es aquella cuya regla está definida por una expresión algebraica, es decir, una combinación de variables, constantes y operaciones algebraicas como suma, resta, multiplicación y división.
Cómo obtener el dominio, rango y gráfica de una función racional (Algebraica) YouTube

16 unidades · 179 habilidades. Unidad 1 Fundamentos de álgebra. Unidad 2 Resolver ecuaciones y desigualdades. Unidad 3 Trabajar con unidades. Unidad 4 Ecuaciones lineales y gráficas. Unidad 5 Formas de ecuaciones lineales. Unidad 6 Sistemas de ecuaciones. Unidad 7 Desigualdades (sistemas y gráficas) Unidad 8 Funciones.
Representación algebraica de una función Tutorela
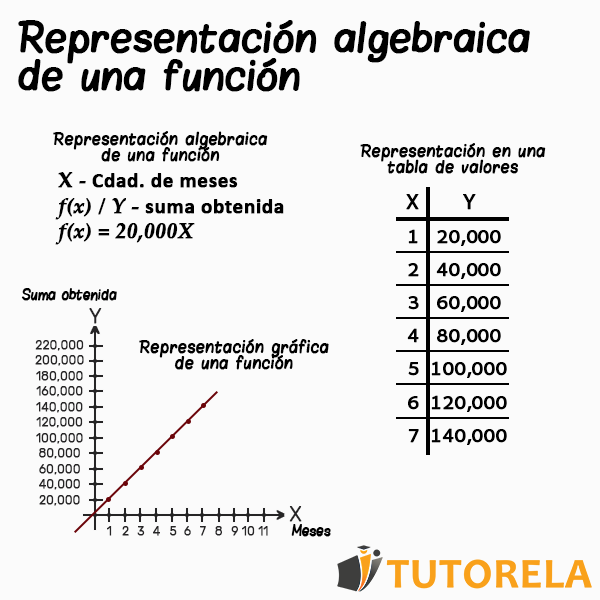
En alguna bibliografías nos encontramos que las funciones algebraicas son aquellas que satisfacen una ecuación polinómica, es decir, cuyos elementos de la función son polinomios o monomios. Clasificación de las funciones algebraicas. Dentro de las funciones algebraicas las podemos clasificar según la características de sus términos en:
Calculando la representación algebraica de una función lineal YouTube

Trataré de plantearte bien sencillo el concepto de función algebraica, a través de un ejemplo que incorpore otros términos usados con frecuencia en relación a este tema, tales como dominio y co dominio de una función.. Para empezar te invito a pensar que el concepto de función lo usamos muchas veces en la vida real. Por ejemplo -algo que conoces muy bien- es lo que te dicen muy seguido.
Funciones en todos lados!!! Función Lineal

Mesas. Una forma de identificar una función algebraica es mediante el uso de una tabla, que puede mostrarnos si hay un dominio y un rango. A veces, las funciones se suman al dominio para obtener el rango, como x + 2. A veces, las funciones multiplican el dominio para obtener el rango, como 3 x.Las funciones también pueden restar o dividir el dominio o usar una combinación de operaciones.